Dans le monde fascinant des mathématiques, il existe un concept qui suscite à la fois l’émerveillement et l’admiration : les fractales. Ces structures infiniment complexes, dont la beauté réside dans leur répétition infinie de motifs à différentes échelles, captivent les esprits depuis leur découverte. Dans cet article, nous plongerons dans le monde envoûtant des fractales, explorerons leur nature, leur histoire et leurs applications, et découvrirons pourquoi elles continuent d’inspirer tant d’émerveillement chez les mathématiciens, les artistes et les amateurs de beauté abstraite.
Qu’est-ce qu’une Fractale ?
Une fractale est un objet mathématique qui présente un motif répétitif à toutes les échelles. Lorsque l’on zoome sur une partie de la figure, on peut constater que cette même partie reproduit fidèlement l’ensemble de la figure, on dit alors qu’elle est « auto similaire ».
Contrairement aux formes géométriques classiques, telles que les cercles ou les triangles, les fractales présentent une complexité infinie et peuvent être générées par des processus itératifs simples. Le terme « fractale » (du latin « fractus » qui signifie « brisé ») lui-même a été popularisé par le mathématicien polono-franco-américain Benoit Mandelbrot dans les années 1970, bien que les concepts de fractales aient été explorés par divers mathématiciens et artistes bien avant cette époque. Mandelbrot en publie les principes avec une très grandes quantité d’exemples :
- modélisation du relief terrestre et lunaire,
- hydrologie,
- structure du poumon,
- granulation des bétons,
- paradoxe d’Olbers,
- turbulences en mécanique des fluides,
- urbanisme des villes,
- distribution des galaxies
Dans son ouvrage qui fait référence, Les Objets fractals – Forme, hasard et dimension, il y présente également des objets jusqu’alors quasiment inconnus :
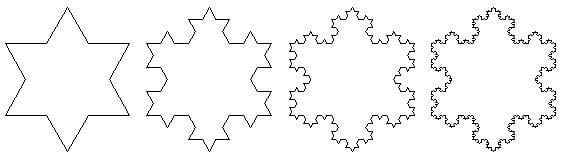
- Le flocon de Koch,
- Le tapis de Sierpinski

Applications des Fractales de la Science à l’Art
Les fractales trouvent des applications dans une multitude de domaines, de la science à l’art en passant par la technologie. En sciences, elles sont utilisées pour modéliser des phénomènes complexes tels que la turbulence, la croissance des plantes, la distribution des galaxies. Dans le domaine de l’informatique et en graphisme, elles sont employées pour créer des paysages virtuels, des textures réalistes, des effets visuels saisissants. En économie, elles peuvent être utilisées pour l’évaluation de risques financiers, pour prévoir des krachs boursiers. Dans le domaine de l’art, les fractales inspirent des œuvres abstraites et visuellement captivantes, qu’elles soient numériques, picturales ou sculpturales.





